今週末の学び方コースは、子ども達と保護者の方たちの許可をもらって1時間長めに開催します。
いろいろな問題を解いてみようと準備しているのですけど、その一つを紹介します。
みなさんも一緒に考えてみませんか。
問題
地面から1m上の位置にぐるりと地球とを取り巻いてヒモを結ぼうと思います。地面にぐるりと巻いたヒモよりどれくらい長いヒモが必要でしょう?
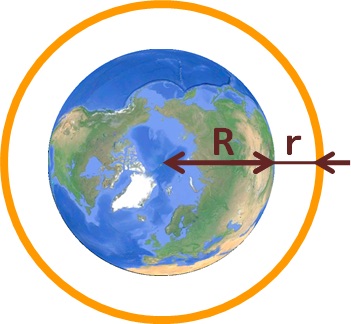
誇張して表現すると下の図になります ⇒ rが1mです。
計算する前に感覚的に、どれくらい長いヒモが必要か
予想してみしましょう。
予想 〔 〕mくらい長いヒモが必要
では計算してみましょう。
※地球の直径は約1万3000km ⇒ 13000000mです。
円周の出し方は
直径 ✕ 3.14です。
3.14というのは四捨五入すると「3」ですから、「3」で計算してみましょうか。
地球の地面にぐるりとヒモを巻くとどれ位のヒモが必要か?
13000000✕3=39000000m … (A)
では、地上から1m浮いた位置にヒモを巻くとどれ位の長さになるか?
直径で考えますから、両端に1mずつ長くなります。
すると直径は13000002mです。
計算しましょう。
13000002✕3=39000006m …(B)
先ほどの(A)との差は
39000006m−39000000m=6m
なんと、たった6mの差しかありません。
地球に巻くヒモに6m足せばいいというのは、わたし的にはびっくりしました。
ちなみに直径がいくら、ということに関係なく「その円周より1m長い円周」というと、6m長いヒモが必要だということになります。つまり、火星の周りであっても、水星の周りであっても、地上1mの距離にぐるりとヒモを巻くと、ということなら6m長いヒモが必要だということになります。
このところも、おもしろいですよね。
賢くたのしい学力向上は
たのしい教育研究所にお任せください
ちなみに、3.14で計算すると 6.28mです。
