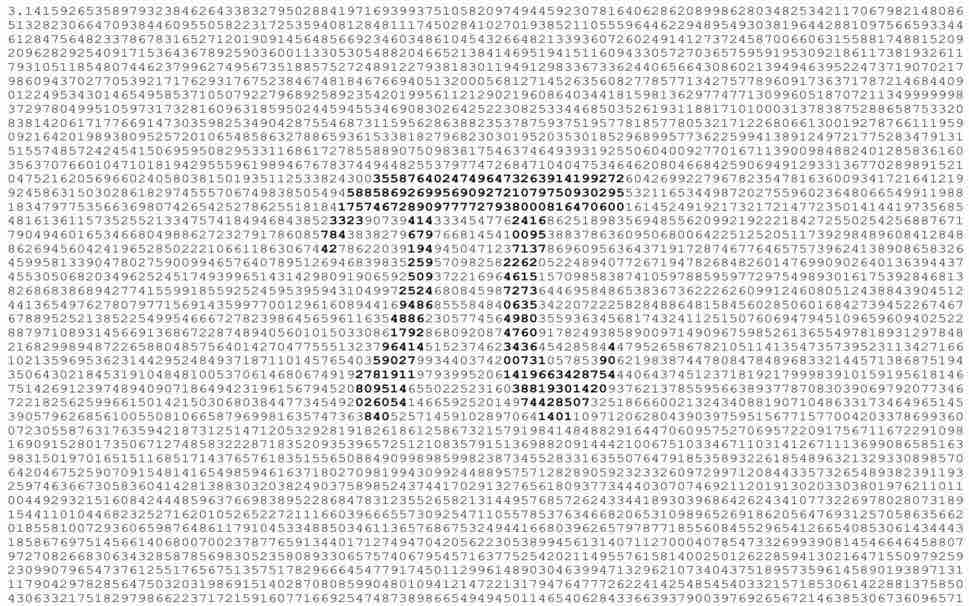大好きなカール・セーガンの話に入る前に、前々回の「ゆとり教育と円周率」について。記事の反響はまだ続いていて、いろいろな質問が届いています。わたしにとってはごく当たり前のことだったのでサ イトに書くのも今頃になってしまいましたが「円周率を3として計算することの素晴らしさ」そのものは、教師になって数年御、高学年をもたせてもらったとき に始まっています。もう二十数年前からのことになります。
この反響からすると、おそらくいろいろな方達が興味を持ってくれると予想できるので、可能な方はぜひ周りの方達に「この記事面白いよ」と伝えて読んでもらうことを提案します。もしかすると「だからゆとり教育はダメなんだ」という意見もあるかもしれませんが、中には子ども達と同じ様な感覚で「おもしろいね」と言ってくれるが出てくるでしょう。そうやって、地道にですけど確実に「たのしい教育」が広まっていくのだと思っています。可能な方はぜひお願いいたします。
さて今回は、わたしの発想法を語る時に重要な人物、カール・セーガンについて書きたいと思います。
わたしはカール・セーガンからとてもたくさんの影響を受けています。
彼が綴った本を繰り返し繰り返し読みましたし、同じ本を何冊も持っています。
地球の生き物や大地の美しさ素晴らしさは星野道夫から学び、星としての素晴らしさはカール・セーガンから学びました。
セーガンは宇宙科学で有名です。
彼が一般の人達に向けて作成したTV番組に「コスモス」があります。レンタル屋さんでは見たことがないのですが、DVDは販売されています。
名作です。
教師時代に、教材として購入してたくさんの子どもたちに観てもらいました。
※わたしが購入した頃は2万円を超えていたのですけど、かなり安くなっていて、DVD7枚パッケージで、書いている今現在で1万円を切っています。日本語字幕もついています。
その中の一部、しかもとても感動的な部分がyoutubeで視聴できます。
それが Pale blue dot. です。
地球のことです。
セーガンの本のタイトルにもなっています。
観測の役割を終えた探査機ボイジャーが太陽系の端に到達しようとする時、NASAのボイジャーミッションにも関わっていたセーガンが「ボイジャーを地球の向きに回転させて、写真を撮ってもらおう」と提案しました。
遠く離れた探査機にうまく命令を伝えられるか。無理な体勢変換で、その後、太陽系を無事飛び出ると期待している流れに影響がでないか。そもそも地球が写るのか?
いろいろな反論があったでしょう。
しかしNASAは最終的にセーガンの提案を受け入れボイジャーのカメラを地球に向けました、さすがです。
セーガン自身がその画像を感動的な言葉で伝えてくれています。
ぜひごらんください。ほんの3分少しの時間です。
動画を見るのが難しい方もいるかもしれません、ボイジャーが振り向いて撮った写真も載せておきます。この右側の茶色の帯の中ほどやや下がわにある点が地球、Pale blue dot. です。

wikipediaに感謝して
この距離から見ると、地球というものは、さして興味深い場所には見えない。
しかし、私たちにとっては違う。
この点をよく見てほしい。
あれがここだ。
あれが故郷だ。
あれが私たちだ。ここにすべての人が住んでいる。
愛する人も、知人も、友達も
いままでに存在したすべての人が、
みなここで人生を送っている。喜びも悲しみも、自信たっぷりの幾多の宗教も
政治思想も、経済主義も、
すべての狩人も、牧人も、英雄も、
卑怯者も、文明の創設者も、破壊者も、
すべての王様も、農民も、
愛し合う夫婦も、すべての父と母、
希望にみちた 子ども、
発明家、そして探検家、
道徳を教える先生も、腐敗した政治家も、
スーパースターも、偉大な指導者も、すべての聖者も、
罪人も、人類の歴史上すべての 人が、ここに住んでいる。
太陽の光照らされた、塵にもひとしいこの場所に。地球は、とても小さな舞台だ。
広漠とした宇宙の中では…
考えてみてほしい。
すべての将軍や皇帝が、勝利と栄光の名のもとに
流した血の河を。
この点の、そのまたごく一部の、
つかの間の支配者となるために。考えてみてほしい。
この点の片隅にいる住人が、
別の隅にいる ほとんど見分けのつかない住人にたいして、
どれほど残虐な仕打ちをしてきたのかを。
どれほど多くの誤解があることか。
どれほど熱心に、人は殺し合うことか。
どれほどの激しい憎しみがあることか。私たちの気どった態度、思いこみによる自惚れ、
自分たちは特別なんだという幻想。
この青白い点はそのことを教えてくれる。私たちの惑星はこの漆黒の闇に囲まれた、
ひとかけらの孤独な泡にすぎない。この広漠とした宇宙では、私たちは名もない存在だ。
他に助けてくれる人はいない、私たち自身をのぞいては。
地球は、現在までに知られている生命をはぐくむ
唯一の星だ。すくなくとも近い将来、
ほかに人類が移住できるような場所は存在しない。行くことはできるか?
たぶん。
住むことはできるか?
いや、まだ。好き嫌いにかかわらず
いまのところ地球が私たちの住む場所だ。天文学は、人を謙虚にし、
身のほどをわからせる学問だという。
人間の思い上がりを示すのに、これほどふさわしい例もないだろう。
私たちのちっぽけな世界を、はるか彼方からみた景色ほどには。
私にとって、この映像は
私たちの責任を表しているように見える。
もっとお互いに気を配り、この青白い点を大切にするとい う責任を。
私たちの知っている、ただ一つの故郷を。
“想像力なくしては、私たちはどこへも行けない”
カール・セーガン(1938~1996)
アナウンサーではありませんが、カール・セーガンの言葉は聞きやすくて、英語の教材にもなると思います。
残念ながら中学生に英語を教えるという機会はまだありませんが、わたしなら、この3分ほどの教材を英語に使います。きっと子ども達も、この言葉のどれかに感銘をうけて、そのフレーズを覚えてくれるのではないかと思います。
興味のある方のために、英文も載せておきます。
From this distant vantage point,
the Earth might not seem of any particular interest.
But for us, it’s different.
Consider again that dot.
That’s here, that’s home, that’s us.
On it everyone you love, everyone you know,
everyone you ever heard of,
every human being who ever was, lived out their lives.
The aggregate of our joy and suffering,
thousands of confident religions, ideologies,
and economic doctrines, every hunter and forager,
every hero and coward, every creator
and destroyer of civilization, every king and peasant,
every young couple in love, every mother and father, hopeful child, inventor and explorer,
every teacher of morals, every corrupt politician,
every “superstar,” every “supreme leader,” every saint and sinner in the history of our species lived there
—on the mote of dust suspended in a sunbeam.
The Earth is a very small stage in a vast cosmic arena. Think of the rivers of blood spilled by all those generals
and emperors so that, in glory and triumph,
they could become the momentary masters
of a fraction of a dot.
Think of the endless cruelties visited
by the inhabitants of one corner of this pixel
on the scarcely distinguishable inhabitants
of some other corner, how frequent their misunderstandings, how eager they are to kill one another, how fervent their hatreds.
Our posturings, our imagined self-importance,
the delusion that we have some privileged position
in the Universe,
are challenged by this point of pale light.
Our planet is a lonely speck in the great enveloping
cosmic dark.
In our obscurity, in all this vastness,
there is no hint that help will come from
elsewhere to save us from ourselves.
The Earth is the only world known so far to harbor life. There is nowhere else, at least in the near future, to which our species could migrate. Visit, yes. Settle, not yet. Like it or not, for the moment the Earth is where we make our stand.
It has been said that astronomy is a humbling
and character-building experience.
There is perhaps no better demonstration
of the folly of human conceits than this distant image
of our tiny world.
To me, it underscores our responsibility
to deal more kindly with one another,
and to preserve and cherish the pale blue dot,
the only home we’ve ever known.
–Carl Sagan, Pale Blue Dot, 1994
たのしい教育は感動を伝える教育です。
日々元気に活動する「たのしい教育研究所」です。
① 毎日1回の〈いいね〉クリックで「たの研」がもっと強くなる!⬅︎応援クリック
② たのしい教育を本格的に学ぶ〈たのしい教育メールマガジン-週刊/有料〉を購読しませんか! たのしい教育の実践方法から発想法、映画の章ほか充実した内容です。講座・教材等の割引もあります(紹介サイトが開きます)
③ 応援として〈SNSや口コミ〉でこのサイトを広げていただければ幸いです!