小学校六年生向けに「学び方特訓」をしている時、「これはいい」と思う教材をたくさん集めていました。

たいていのそういう中から
「限られたコースの時間で、今この子たちに伝えたい内容は何か」
ということで問題を精選していくので、半分以上はお蔵入りになります。

そういう、利用しなかった教材を整理していると
「これはやはりいいな」と思えるものもたくさん出てきます。

きっと、わたしの「学び方コース」を受講してくれた六年生も見てくれると思いますし、その子達だけでなく、教育に関わるいろいろな方達にも見ていただきたいのでここに掲載します。

　学校や家庭で問題を出したり、自分の頭を鍛えるつもりで試してみるといいと思います。
※解く時に利用する「円の面積の公式」は小学校５年生で出てきます

もんだい
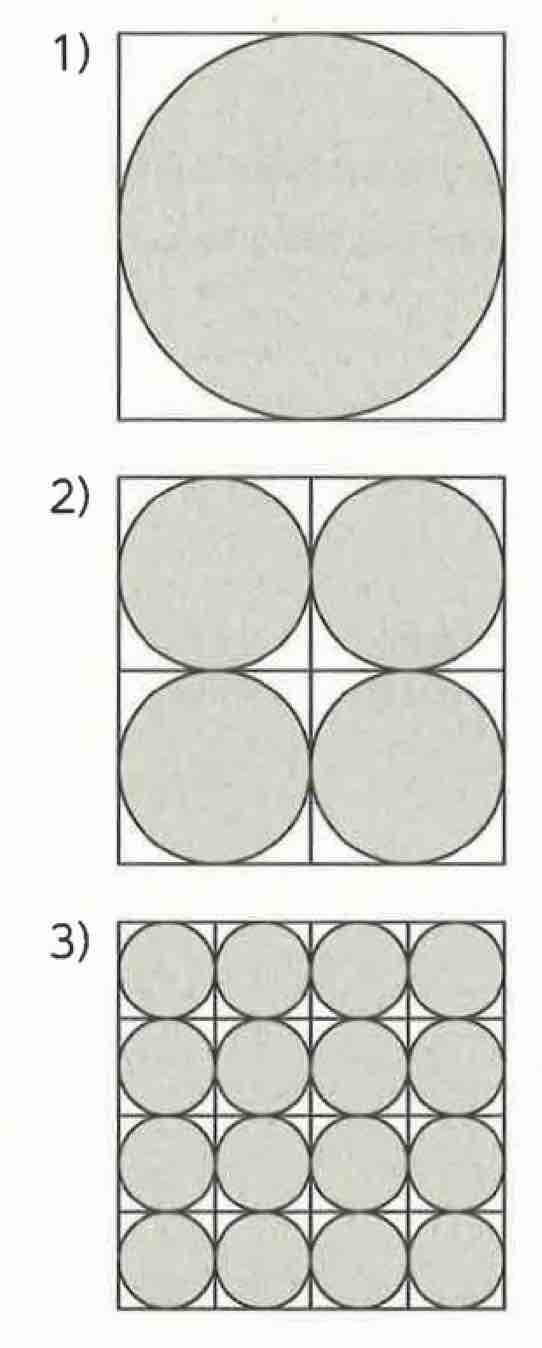
同じ大きさの正方形が三つあって、それぞれに円が描かれています。
描かれた円の面積が最も大きくなるのはどれでしょう？

 

予想
　ア．1)の円の面積が最大
　イ．2)の円の面積の合計が最大
　ウ．3)の円の面積の合計が最大
　エ．その他

予想をたてたら計算してみましょう。

計算のヒント
正方形の一辺の長さを勝手に ○ cmというように決めてしまうといいですよ

※ 解答編 ※

１辺を８cmの正方形だとしましょう。

解説　なぜ8cmにしたか
円の面積を出すには　半径×半径×円周率(π)です。
正方形の１辺を８cmにすると3)の図形の半径は整数「1」で表わすことができますから、おそらく計算が楽です。
もちろん、正方形の一辺は１cmでも４cmでも計算は可能です。

まず3)の面積の合計から
正方形が縦横４つずつに仕切られているので、小さな一つの正方形の１辺は２cmです。

すると小さな円の半径はその半分の１cmですね。

半径×半径×π＝１×１×π＝π　※つまり約3.14

これが16あるので
あわせて １６π  ㎠

2)の円の面積の合計はどうか
さっきは自力で解けなかったけど、ここまで読んで自力で解けそうだ、という人は挑戦してみましょう。

計算中

計算中

こうです。
大きな正方形の１編が８cmですから、仕切られた４つの部屋の一辺は４cmです。
すると円の半径は２cmになります。
一つの円の面積は

２×２×π＝４π

これが４つあるので
４×４π＝１６π　cm２

おやおや、３）と同じになってしまいました。
ということは、１）も同じになるのでしょうか？

やってみましょう。

1)の円の面積

半径は４cmですから
４cm×４cm×π＝１６π

おやおや、三つとも一緒になりました。

つまり正解は　エその他　


「三つとも同じ面積になる」が正解です。

みなさんの予想はどうだったでしょうか。

私の直感は
３）がもっとも面積が大きくなる、でした。
なぜか？
どんどん細く分けていけばまるでパソコン上のドットの様に「ほとんどん全部が円だ」というようになってしまう　と思ったからです。

しかしその直感は間違っていました。

「直感はよく間違うことがある」と感じると同時に

「その直感の間違いを教えてくれるのが《学ぶ》ということである」
と感じました。

ということで、わたしが感動した一問をおとどけしました。

沖縄のたくさんの子ども達の学力を本気で考える
「たのしい教育研究所」です