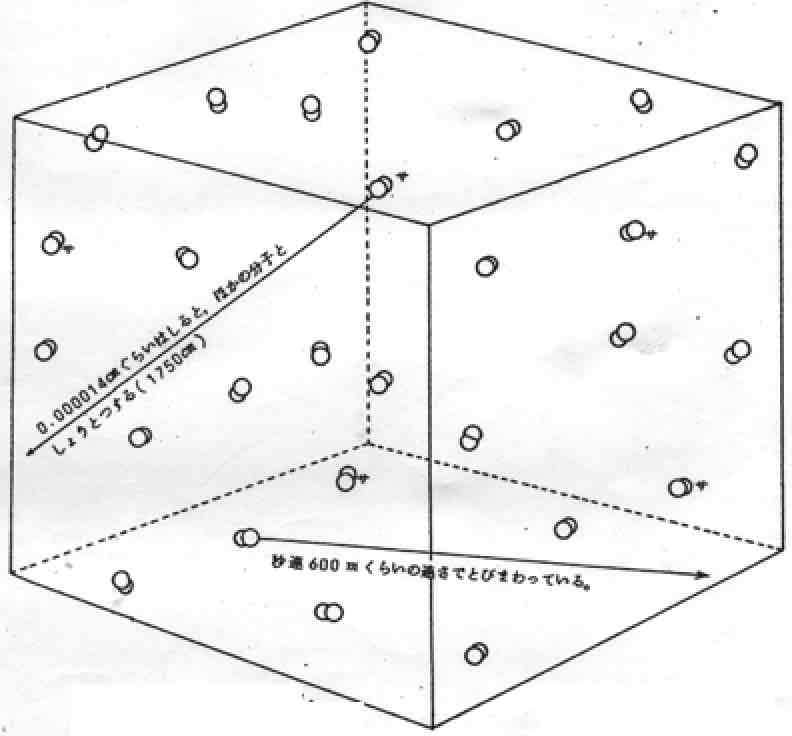
前に書いた「鬼怒川決壊を原子論的に見る」という話は、予想以上の反響がありました。
その中でも、科学的・原子論的な見方考え方を小学生にしっかり伝えられるのだという事に興味・関心を持ってくださった方たちがたくさんいた事に、意を強くしています。

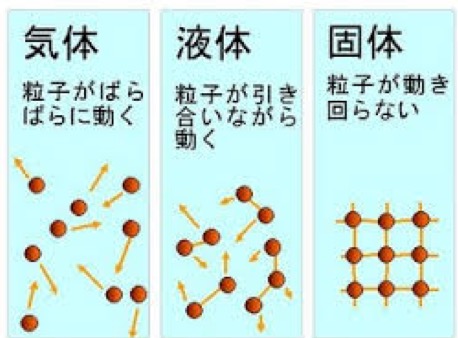
たのしい教育研究所に、こういうパネルがはってあります。

あらゆることを「原子論」で考えることが基本中の基本！
－算数も理科も社会も国語も医学も宇宙も人生も－

今回は、「原子論」について書かせて頂きます。

科学的な見方・考え方の重要性をいろいろなところで語っていますが、その科学の中でも最もより処となる見方・考え方が「原子論」です。
「予想を立てて確かめる」ための基本となるのが『原子論』だという事ができます。
つまり、予想を立てる時に「原子論で考えるとどうなるのか？」と問いかけてみることが、とても大切だということです。

「鬼怒川決壊」について書いた様な自然科学的なものだけでなく、数のイメージ・図形のイメージでものごとの本質を探る『算数・数学』でもそうです。

私は、１．２．３という数そのものを「原子」だとみる見方・考え方で授業することがありますが、とても有効な方法です。
いつかプラン化して、いろいろな方たちが利用できるようにしたいと思っています。

たとえば「数の原子」という見方をすると、大きな数も「数の原子／できるだけ小さな数」で表してあげることができます。すると、数のイメージをとてもつかみやすくなります。

　たとえば地球から太陽までの距離はおおよそ　150000000km  です。
 「指数」という表現方法を利用して、できるだけ小さな数の組み合わせてでみると

と表すことができます。
小数点のうしろに「0」が８つ続きます、という表し方です。

地球から月までの距離はおおよそ  380000 km です。
これは

と表すことができます。
距離の違いを０の数や、その前の「1.5」「3.8」の比較でイメージできます。

人間の赤血球は直径が「1mの1万2500分の1」くらいです。
これもできるだけ簡単な数の原子の組み合わせでみてみましょう。

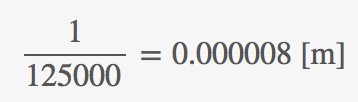
です。

それをさっきの様に「指数」で表現すると

と簡単な数の組み合わせで表現できます。

これは、８の前に０が６つある、ということを表しています。
たとえば白血球の大きさや原子分子の大きさとくらべてどの程度違うのかをイメージするときにとても有効です。
0.000000…　という様な０がたくさん続く数字はイメージしにくいので、科学者たちは、こういう表現方法で、とても小さな数やとても大きな数を表すことが多いのです。

　社会でも、原子論的な見方は有効です。

　もともと人間も原子でできているわけですから、社会では、その塊の人間一人を「原子」だと想定してながめる、という見方・考え方です。
これについては、またいつか項をあらためて書かせて頂きます。

　たのしい教育研究所で「原子論的な見方・考え方」をいろいろな方たちに伝えて行きたいとおもっています。

沖縄の教育に全力投球
たのしい教育研究所です

以前このオフィシャルサイトで紹介した
「ぼくのジィちゃん」
を、学び方コースの子どもたちにも聞いてもらいました。

子ども達にも大受けでした。

家庭で、食事の後とかに読んであげたり、寝るときに読んであげたりするのも、きっと喜ばれると思います。

本のたのしさと可能性も
たのしい教育研究所の守備範囲です
沖縄をもっとたのしく賢く
たのしい教育研究所です

保護者の方達からの要請で個人的に開催を決断した「子ども達対象の学び方コース」ですが、いろいろな方が関心を持っていただけているようです。

少人数だということ、小学校六年生のみということは、なぜかという声もありました。
一生ものの力を身につけてもらいたいということ、それから、中学受験レベルの子ども達を対象とするためです。

学び方の大きな基本は、書くと簡単です。
「予想を立ててたしかめる」ということです。

まず、いろいろな課題や問題に予想を立てる。
そして丁寧にそれをたしかめる。
その流れです。

それなら簡単だと思うもしれません。
もしもそれが簡単に身につくならすばらしいことです。

国語でも算数でも理科でも社会でも、全てその流れが大切です。

これは一生ものです。

何か新しい課題を前にした時、その流れで前に進んでいけるからです。

研究所では、それを一人ひとりに丁寧に指導しています。
この子たちの伸びがたのしみです。

沖縄の実力ある子ども達の教育
たのしく豊かな子ども達の育成に
全力投球の「たのしい教育研究所」です。

マスコミから流れる情報から遠い生活をしている私も、今回の鬼怒川決壊は、とてもつらいおもいをしながら見ています。
3.11の大地震の後、居ても立ってもいられず、気仙沼ではまだ炎が収まっていない状況の中、テントを背負って飛んでいった日の事を思い出しています。

被害でつらい思いをしている方たちの事を思い、こういう災害を少なくしていくために、科学的に物事を見ていくことのできる人たちが増えていくことは不可欠です。

「学び方コース」でこういうお話をしました。
少しその事を書かせて頂きます。

今回の鬼怒川決壊に関連して、『水の力はすさまじい』という言葉を異口同音に耳にしています。
これはしかし
『水』だから恐ろしい
のではなく
『大量の原子が絶え間なくぶつかってくる』
から恐ろしいのです。

小学校の理科で「三態変化」を学びます。
簡単にいうと、私達の周りの原子は、
温度の状態で「個体」「液体」「気体」の3つの状態に変化する
ということです。

そしてそのイメージを、こう説明している図をよく見ると思いますが、実はこれを見ていると勘違いしてしまいます。
　同じ体積なら、そこに存在する原子の数が同じように感じてしまうからです。

実は、「気体」と「液体・個体」では、そこに存在する原子の量が「とてつもなく」違います。

気体はすき間（真空）の中をわずかな原子が飛び回っています。

私が個人的に好きだという事だけでなく、「原子論を教育する時の原点」であると断言してよい絵本があります。

もしも原子がみえたなら―いたずらはかせのかがくの本
(いたずらはかせのかがくの本 新版)

その中の絵を見てみましょう。

気体はこういうイメージです。
針の先でほんの小さくつついたよりももっと小さな一点を拡大してみましょう。
ずいぶんたくさんのすき間（何もない空っぽ／真空）の中をわずかな空気の原子・分子（原子がくっついた分子の状態）が飛び回っています。

これは0.000001 cmを拡大してイメージした図です。これを見ているメディアによって表示される大きさが異なるので、詳しい方からすると「縮尺的に変だ」と感じる人もいるかもしれません。しかしあえて「こういう目でみたかの様なイメージを持つことができる」ということも「学ぶ力」です。

では、液体はどうでしょうか？
「液体」と「固体」では原子や分子(原子が組み合わさったもの)の量はあまり違いません。どちらも原子・分子同士が隣りどおしくっつき合っているからです。

液体のイメージはこうです。
ほんの一滴の水をさっきの様に拡大してみた図です。

液体から少し離れて自由にとびまわりはじめたものが「気体」です。
気体と液体・個体では、そこに存在する量がとてつもなく違う、ということが伝わるでしょうか。

今回の項は今回の鬼怒川決壊で『水の力はすさまじい』という言葉を耳にするという話からはじまりました。
そこに戻りましょう。

たとえば家・建物にぶつかってくるものが「気体」の『空気』であった場合と「液体」の『水』であった場合には、「それが空気だから、水だから」ということではなく

◎絶え間なくぶつかってくる原子の量がとてつもなく違う
　⇒ 破壊力が比較にならない程大きい

ということなのです。

たのしい教育研究所は『沖縄』にあります。
沖縄は海が近いので、大量の水が山から流れ込んで来ても、それが比較的早く海に流れてしまいますから、洪水の被害は少なくてすみます。
その沖縄では「台風」はとても大きな災害の一つです。
毎年の様に被害があります。
台風は「気体」のスピードが増加することに伴う災害です。

しかし水は「液体」ですから、もともと持っている破壊力がすごいのです。

防災に関して単純に比較はできないといいつつも、そのものが持つ破壊力ということで考えれば「より怖いのは液体が激突してきた時である」ということです。
そこに存在する原子の量がとてつもなく違う、つまり破壊力が違うのです。

液体がぶつかってくるという事は、原子の量で言えば、固体がぶつかってくる、つまり大きな岩石・土砂などが絶え間なくぶつかってくることとあまり差がないのです。

「津波」はこの液体が、台風並みのスピードで押し寄せてくるわけですから、さらにすさまじい破壊力になります。

小学校で学ぶ三態変化が『原子論』的にいきいきとイメージできる様になれば、ここで書いた内容であっても、小学校低学年の子ども達、いやもしかすると保育園の子ども達でも理解できる様になると思います。

たのしい教育研究所の授業は、そういう本格的なものを、子どもたちだけでなく、いろいろな方達に伝えたいのです。

今回は「学び方コース」で取り上げる内容を書かせて頂きました。
日を改めて、その②として「川の作り」から見た今回の災害について科学的にみていくことにします。

教育に全力投球
力のある子ども達を着実に育てる
たのしい教育研究所です