パパヤの品種改良の話に興味をもってくれた読者の方から丁寧なお便りが届き、その中に品種改良と進化の違いについて知りたいという話がありました。それについて書いてみましょう。正確さより、イメージが伝わることを優先して細かいところは端折ります。
生物は〈分裂〉といって、自分のコピーを作って生きていくタイプがいます、原始的な状況ではほとんどの生物がそうでした。そのスタイルを今も残している生物がいるわけです。ウイルスがそうです、菌類もそうです。下の写真はコロナウイルスです、人間の体内でどんどん分裂して増えていきます。
単細胞生物のアメーバも分裂・コピーで増えていきます。
シンプルな体の作りをしている〈単細胞生物〉ただけでなく、多細胞生物の中にも分裂(コピー)して増えていくタイプがいるんですよ。
これはこのサイトでも以前取り上げたベンケイソウです。ベンケイソウはタネで増える方法と、葉の周りに自分と同じコピーを作って増えていくという二つの方法で増えていきます。

どんどん成長して一つのベンケイソウ(セイロンベンケイ)となっていきます。
 https://gakusyu.shizuoka-c.ed.jp/science/sonota/ronnbunshu/R3/213086.pdf
https://gakusyu.shizuoka-c.ed.jp/science/sonota/ronnbunshu/R3/213086.pdf
そういう様に〈分裂〉で増えていくのではなく、私たち人間をはじめ、多くの多細胞生物たちは〈有性生殖〉といって、オスメス二つの性質をまぜあわせて子どもをつくります。
二つの性質が混ぜ合わさって子どもができていくので、そこには多様な性質が生まれます。
たとえば犬の場合、白い犬、黒い犬、大きな犬、小さな犬、よく吠える犬、静かな犬、ある病気に強い犬、弱い犬など、書ききれないほどたくさんの性質が広がっていくわけです。
前に書いたパパヤについてみていきましょう。
パパヤにできるたくさんのタネが成長していく中で、背の高いパパヤ、低いパパヤ、細いパパヤ、太いパパヤ、実が甘いパパヤ、甘くないパパヤ、葉が大きいパパヤ、小さいパパヤなどとてもたくさんの性質がそこに出てくるのです。
たとえば成長しても比較的小さなパパヤ同士を交配(雄しべの花粉を雌しべの柱頭に受粉させる)させると、実ができて、その身の中にはたくさんのタネができます。
 そのタネから成長していくパパヤもまたいろいろな性質をもったパパヤになります。
そのタネから成長していくパパヤもまたいろいろな性質をもったパパヤになります。
その中には以前のパパヤより身長が低い株も育つでしょう。
そうやって〈低いもの同士〉を何世代にもわたって交配させていくと、前に紹介した様な、こんなに低いパパヤもできていくのです。

これを〈品種改良〉といいます。
つまり「人間の目的によって育てあげてきた品種」ということです。
現在たくさんの種類に別れた犬たちは、もともとオオカミの子孫です。体の大きなタイプ同士、毛の長いもの同士、短いもの同士etc. いろいろな特徴を持つもの同士を交配させることによって、こんなにたくさんの種類に分かれてきました、品種改良です。
 品種改良は今の所、同じ〈種〉たとえば犬なら犬の仲間の中で、パパヤならパパヤの中で多様化した品種を生み出しているだけで、新たな種を生み出すような段階ではありません。
品種改良は今の所、同じ〈種〉たとえば犬なら犬の仲間の中で、パパヤならパパヤの中で多様化した品種を生み出しているだけで、新たな種を生み出すような段階ではありません。
ではこういう品種改良は〈進化〉とは違うのでしょうか?
品種改良は私たち人間が、いろいろな目的で自分たちの都合の良いようにコントロールしてきたものです。
それに対して〈進化〉は生物の子孫たちが周りの環境に適したり、子孫を残しやすいものたちが生き残っていった結果、多様化していくことです。何十万年何百万年という長い歴史の中で、ウイルス・アメーバー・菌類のようなシンプルな生物が進化して、鳥やクマ、魚や人間といった多彩な生物が生まれて行きました。
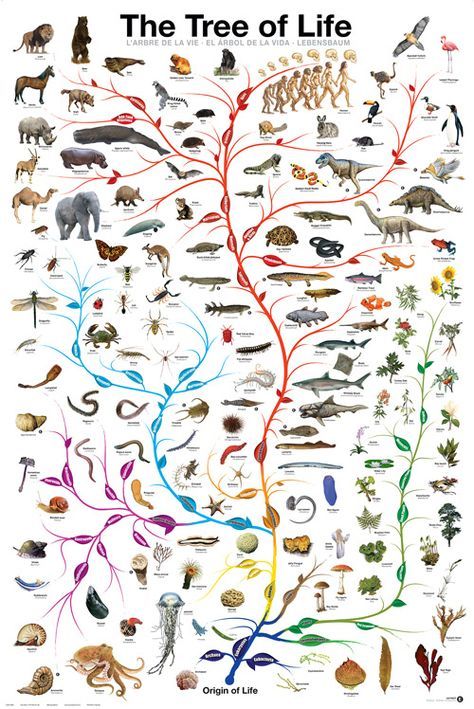
シンプルな生物から私たち人間が生まれるまで何十億年という時間が流れていきました。これが進化です。

進化という大きな流れの中で多様化していった生物の、たとえばネズミをとりあげて、毛が短いもの同士を掛け合わせ(交配させ)て、ほとんど毛の無いネズミを生み出したりしているのが〈品種改良〉です。
品種改良と進化について、前よりもイメージができてきたでしょうか。
さらに話を続けたいのですけど、長くなったので、ここで一区切りつけておきましょう。次回もおたのしみに。
たのしい教育全力疾走RIDE(たのしい教育研究所)、みなさんの応援が元気の源です。一緒にたのしく賢く明るい未来を育てましょう。このクリックで〈応援〉の一票が入ります!