自由研究講座の中の「いっきゅう先生のワクワク宇宙教室」を受講したお母さんから、とても楽しかったです、という言葉に続いて、次のような話がありました。

　古代ギリシャの科学者が「あんなに大きな太陽が、小さな地球を回っているなんておかしい」と考えたという視点に驚きました。

　ところで、そもそもどうして、月の大きさくらいにしか見えない太陽が地球より大きいと分かったのですか？

　ここではアリスタルコスの発想法について、さらに研究を深めたい方たち向けの内容として紹介したいとと思います。
　アリスタルコスの考え方をたどると、サイン・コサインなどの三角関数や、三平方の定理などが必要になるので、そこはいつか学んでもらうとして、それでも中学校くらいの勉強の内容で、計算することができることは理解できるのではないかと思います。
　おつき合いください。
　

　アリスタルコスはまず、月と地球の大きさの検討をつけました。
　どうしたか？

　〈月食の時の月〉の様子から検討をつけたのです。
　この図はアリスタルコスの唯一残っている著書「太陽と月の距離と大きさについて」の写本です。※写本＝その頃は印刷する技術が無かったので一冊ずつ手書きで写し取っていた

　左が太陽、真ん中が地球、右が月の概略図です。

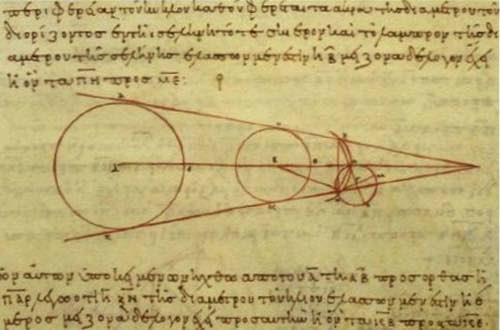
アリスタルコス「太陽と月の距離と大きさについて」写本　wikipedia

　アリスタルコスは、月食つまり〈月が地球の影の中を通過する様子〉から地球の直径は月の直径のおおよそ３倍であると検討をつけました。

　次に太陽の大きさです。

　この図を見てください。
〈半月〉つまり、地球から見て月の半分が明るい時は〈地球・月・太陽で描く図形〉が「直角三角形」になります。

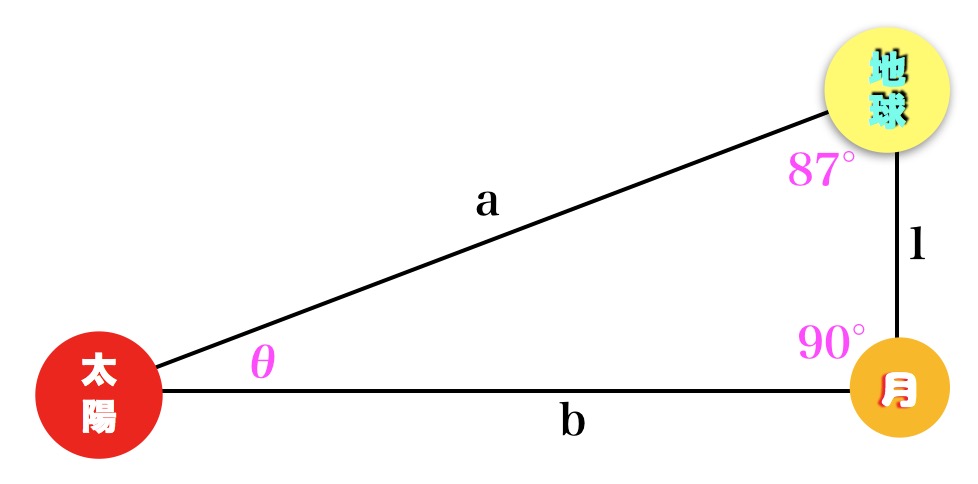
　直角三角形を描くと〈三角関数〉が簡単に利用できます。
　〈三角関数〉というのは、アリスタルコスより前のユークリッド、ピタゴラスが利用した数学技法です。アリスタルコスはユークリッドの弟子だったという話もあるくらいで、三角関数のアイディアは持っていたにちがいありません。

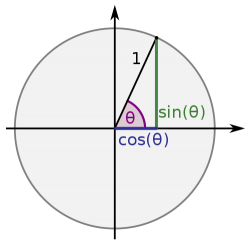
　アリスタルコスは太陽・地球・月の描く角を〈８７°〉だと算出しました。
　すると、太陽との角度θは〈３°〉になります⇨三角形の内角の和は１８０°だから。
　地球から月までの距離を〈１〉だとすると、三角比で １／ａ≒０.０５（ｓｉｎ５°）だとわかります　※三角関数で算出
するとａ≒１／０.０５≒２０
つまり地球から太陽まで（ａ）の距離は、地球から月まで（１）の２０倍だと計算できます。※今の正確な計算では４００倍だとわかっています。アリスタルコスが測定した角度が少し小さかったので、距離に大きな差がでてしまいました。しかし数字は違っていても、何倍も遠くにあることを力技で計算したところがアリスタルコスのすごさです

　実際のフィールドで、月までより２０倍のモデルを置いて、月と同じくらいの大きさに見えるには、どれくらい大きくないといけないのか考えたのでしょう。

　２０倍遠くても同じ大きさに見えるとすると、大きさも２０倍ないといけないことがわかります。
　地球は月の３倍だから、太陽は地球の直径のおおよそ６倍くらいになる。※実際は１０９倍
　直径が６倍だということは、球の体積で計算すると、重量は３００倍も大きいことになる。※現在の科学的なデータで計算すると〈太陽は地球より約３３万倍

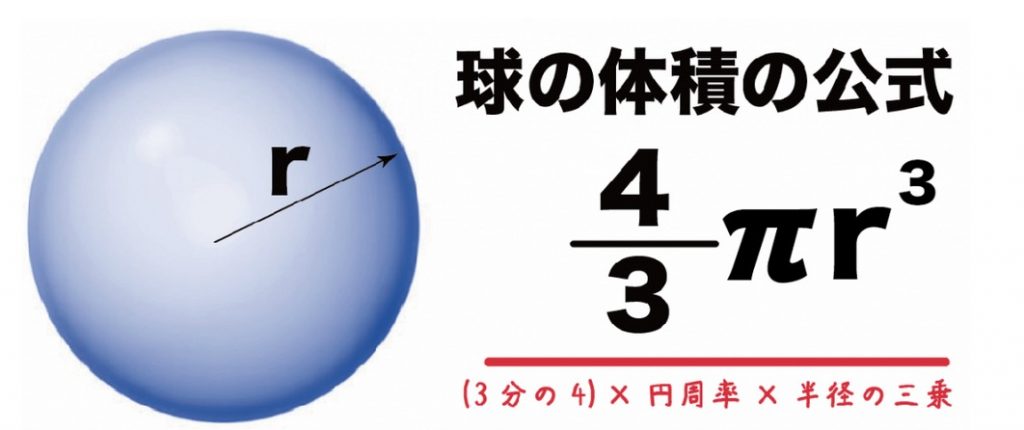
　アリスタルコスの頃はπの値は定まっていませんでしたし、現在の計算からみると違っているとはいえ、しかし、球の体積はおおよそこうだろう、という様にして「太陽は地球よりはるかに大きい」ことを正しく予測したのです。

　この結果からアリスタルコスはこう考えました。

　３００倍の大きのものが、この小さな地球の周りを回るだろうか？
　たとえば小さな子どもと大人の大きさのでも６～７倍くらいの違いだ。
　小さな子どもと大人がヒモでお互いをふり回すとして考えてみると、小さな子が大の大人をふり回すなんてできない。
　大きな大人が、小さな子どもを振り回すのが普通だろう。
　６～７倍ですらそうなのだから、自分より３００倍くらい大きなものを回すなんて有りえない。
　地球の周りを巨大な太陽が回っているのではなく、太陽の周りをちっぽけな地球が回っているに違いない。

　アリスタルコスは、そういう思考過程を重ねて地動説をとなえる様になったのです。
　数字的には間違っていましたが、地動説そのものは引き継がれ、ガリレオの金星の観測によって、天動説の間違いと地動説の正しさを証明されました。

　人間が真理を見つけていく過程のダイナミックな歴史を感じませんか。
　今わからなくいても、興味をもっていれば、きっとまたいつかこのことを思い出して、自分でもアリスタルコスのことを調べてみたくなると思います。
　興味関心のあることをどんどん調べて賢くなっていってくださいね。
　毎日たのしく自由研究、ＲＩＤＥ（ ライド：たのしい教育研究所 ）です。この〈いいねライン〉をクリックすることで〈たのしい教育研究所〉への「応援票」が入ります☆いいね☆