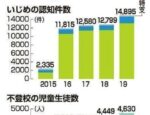
〈たの研〉に来る保護者の方たちからの相談には、ゴールデンウィーク前後から不登校の相談が増えてきます。その中で「去年まではそういうことはなかったのだけど、新しい先生になってから〈勉強がおもしろくない〉〈授業がわからない〉という様になった」と話す方が一定割合います。
カウンセリングの話はまたの機会にして、授業の話を書かせてください。
公立学校の授業で扱う内容は〈学習指導要領〉に書かれていて「教えることになっている」と教師は考える、その感覚は「はい、今日は教科書の◯ページです」という言葉にも表れて、そこから伝わる〈やることになっている感〉ははっきりと子ども達の心に刻まれます。
教師の〈やることになっているからやる〉というスタンスは「あればあるでよいけれど、〈たのしさ〉は特に無くてもかまわない」という発想にもつながります。
しかし指導要領の根幹は「主体的・対話的で深い学び」です、〈やることになっているからやる〉というのを「主体的」とはいいません。
この矛盾をどうしたらよいのでしょう。
学習指導要領について編成側の〈文科省〉の説明をみてみましょう。※下線はいっきゅう
「学習指導要領」では、小学校、中学校、高等学校等ごとに、それぞれの教科等の目標や大まかな教育内容を定めています。
また、これとは別に、学校教育法施行規則で、例えば小・中学校の教科等の年間の標準授業時数等が定められています。
各学校では、この「学習指導要領」や年間の標準授業時数等を踏まえ、地域や学校の実態に応じて、教育課程(カリキュラム)を編成しています。
https://www.mext.go.jp/a_menu/shotou/new-cs/idea/1304372.htm
学習指導要領で定めているのは〈大まかな内容〉であり、各学校では〈地域や学校の実情に応じてカリキュラムを編成〉していると記しています。
ところで学習指導要領は法律ではありません、それより遥かに拘束力の高い〈学校教育法〉には
教諭は、児童の教育をつかさどる。
学校教育法第 37 条第 11 項
とあります。
学習指導要領に記された大まかな内容を、子ども達が主体的・対話的に深く学ぶ、その教育を先生が司るのです。
教科書は学習指導要領の大まかな内容を具体的に例示したテキストです。そこでも〈やることになっているからやる〉という感覚は、主体的・対話的で深い学びと矛盾してきます。
〈やることになっているから学ぶ〉VS〈主体的に学ぶ〉
いったいこの矛盾をどうすればよいのか?
その矛盾を解くカギが〈たのしさ〉です。
まず自分が学ぶことをたのしむ。教師自身の個性が輝いていくことで、こども達にもたのしさが伝わっていくでしょう。
「さぁみんな、今日のさんすうは〈並べ方を考えよう〉だよ、たのしんでいこうね」
ニコニコした表情でそう伝えることができたら、これまでと違う扉が開くはずです。
具体的な問題で考えてみましょう。
〈たの研〉で算数の解き方入門をしていると、確率系の問題が苦手だという先生たちがたくさんいることに気づかされます。
確率は漠然とした状況であることを予測する時などとても重要なツールになります。「こっちの危険度とこっちの危険度はどっちが高いか」などを確率的に見ていくことでより安全な状況を選ぶことができます、確率的な見方考え方で命が救われることもあるでしょう。
重要なものを学ぶのがたのしくないわけないのです。
確率的な見方考え方を身につけていく過程で〈並べ方・組合せ方(順列・組合せ)〉が重要なテーマの一つになります。
たとえば1から5までのカードがあります。これをいろいろな並べ方で一列においていくと、何通りくらいの並べ方があるでしょうか?
この四角の中に1から5までの数字を入れていくわけです、12345と並べたり、逆に54321と並べたり。
違う並べ方はいくつなのか小学生の感覚で考えてみてください。
たとえば1の並べ方はいくつか?
一通りです。
1と2の二つのカードを一列に並べる方法は?
1・2 あるいは 2・1 の二通りです。
1と2と3の三つのカードの並べ方は・・・
123、132、213、231、312、321 の6通りです。
こんな風に考えていくと、12345の5枚のカードの並べ方は何通りあるのでしょう。この四角の中に数字が入ると考えてみるとよいでしょう。
ア.5通りくらいうありそうだ
イ.10通りくらいありそうだ
ウ.20通りくらいありそうだ
エ.50通りくらいありそうだ
オ.その他
どうしてそう思いましたか?
⬇︎
考えてみよう
⬇︎
考えてみよう
⬇︎
5枚のカードを並べるだけで〈120通り〉の異なるパターンが出てきます、この多さは、私にとって驚きなのですけど、みなさんはどうでしょう。
計算ができる暗算できるという人は〈答えが当たった〉というそのことで嬉しくなってしまうかもしれません。けれどじっくり考えてみてください、たった5枚のカードで120通りですよ。
もしあと5枚増やして1~10までの10枚のカードを一列に並べようとしたら、〈352万8800通り〉の並べ方があります、全部の並べ方を終えるまでどれくらいの時間が流れていくでしょう・・・
この爆発的な多さに驚くのか、「計算でこうなるからこう」と無感動にテストに答えて終わるのか。
一方が〈たのしさ〉、一方が〈無感動〉です。
指導要領に書かれた内容をたのしく教えることによって、主体的・対話的で深い学びが可能となるのです。
「今年になって勉強がたのしくないというんです」という保護者が出てくるのではなく「うちの子は去年まで学校のことというと友だちのことばかりだったんですけど、今年、先生が担任してくれる様になって、勉強の話をしてくれる様になりました」そういう保護者の方たちを増やしてみたいと思いませんか。
興味のある方は、ぜひたのしい教育研究所で学ぶことをおすすめします。学ぶ方法はとてもたくさんありますが、まず今月は〈初夏の講座〉の受講をおすすめします。
内容は⇨初夏の講座2022
募集が始まり、参加申込みが増えてきました。席には限りがあります、受講したい方はお早めにどうぞ⇨申込みはこちら 〈初夏の講座の申込み〉と記入し、名前・所属・緊急時の電話番号を書き入れて送ってください。お会いできることをたのしみにしています。
たのしい教育全力疾走RIDE(たのしい教育研究所)、みなさんの応援が元気の源です。一緒にたのしく賢く明るい未来を育てましょう。このクリックで〈応援〉の一票が入ります!