メールマガジンを発行すると、その記事に対する感想や評価が届くのがたのしみです。
今回は出して10分くらいたたないうちに二人の方から
「RIDEの今日この頃の章のミツバチの写真がとてもいい」という評価と
「授業の章のサイフォンの原理で自分も魚の水槽の水の入れ替えをしているのですけど、太い管と細い管で比較するとスピードに差が出てくるのではないかと予想しています」
というたよりが届きました。
嬉しいことです。
ということで今回の表紙をおとどけします。

このサイトの読者の方に、メルマガの映画の章のタイトルをチェックして借りに行くという方もいて、時々たよりをもらいます。
うれしいことです。
最新号の映画の章「透明人間 2020年版」もおすすめですよ!
※
今回は〈授業の章〉のサイフォンの簡単な実験を紹介する前に書いた「うまく説明できないことでも子ども達にどんどん見せてあげよう」という話を紹介します。

はじめに
〈意味が説明できないなら授業にとりあげるのはやめた方が良い〉と考えている人が多い様です。
それはとてももったいないという話を何度かしてきました。
不思議だ、面白いなという現象は「こういう現象があるよ、おもしろいよね」という様に、子ども達にどんどん見せてあげたいものです。
私が敬愛するガリレオは弟子たちに、自分ではまだうまく説明できないといういろいろな現象を見せていました。

その一つが〈深い井戸からポンプで水を吸い上げようとしても9mくらいまで来たら止まってしまう〉という現象です。
とても不思議におもったガリレオはその研究に没頭したのですけど、なぜそうなのか解明できません。
ガリレオの死後、その意思を引き継いだ弟子のトリチェリが〈大気圧〉の謎を解き明かしました。

トリチェリは水ではなく〈水銀〉を利用して予想・実験しました。
水だと9mの高低差が必要なのに、水銀は重くて1mも上がらずに止まってしてしまうので予想・実験がスムーズにいきます。 トリチェリは、液体を吸い上げるのは〈大気による圧力である。周りにある空気が液体を下に押していて、それを利用して吸い上げている〉ことを発見しました。一定の気圧の元では決まった高さまでしか液体を吸いあげることができないのです。水銀は1気圧で76cmがその限界です。
水銀と水の密度(1㎤あたりの質量・重さ)の比は〈14:1〉ですから、水がほぼ10mで止まってしまうことも計算通りになります。
ちなみに私は、この〈水銀を使うアイディアの元〉はガリレオが出したのではないかなと予想しています。何しろトリチェリがそのことを解明したのはガリレオが他界して翌年のことですから。まだ調べることができていませんけど、たのしめにとっているテーマの一つです。
「不思議だ」と思ったことを自分の中でとどめずに、それはいろいろな人たちに伝えていくことで、たのしさが広がるだけでなく、社会も豊かになるでしょう。
発想法の章に書きたいことまで広がってしまいました。
ということで今回は、このトリチェリが解明した大気圧とも関わる〈サイフォンの不思議〉についてとりあげます。
このサイフォンの原理は科学的に研究が進んでいますから、科学上の謎だというわけではありません。
これがサイフォンの原理を示した図です。
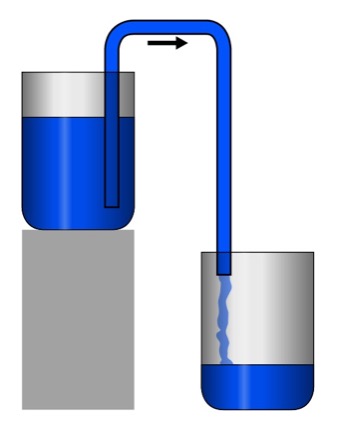
高い位置の液体が満たされた管の中を通って勝手に低い位置に移動してしまう現象です。上の水がいったんその位置より高い位置に上がって、下に降りていくので、見ているとほとんどの人は不思議に思うでしょう。
私いっきゅうも、近所の上級生が魚の水そうの水をかええる時に下においたバケツにサイフォンの原理で水をどんどん移動していたのを見て、とても驚きました。
自宅に帰って自分でホースを使って実験し、簡単に確かめることができたので、今でもその感激を覚えています。
ところが教師になってから、知人がその現象についてめんどうな説明をしたので「もういいよ」とうんざりした経験があります。
十分たのしい現象なのに、あれこれ説明したためにせっかくの興味が失われていくことはあるのです。逆に〈説明が間違っている可能性〉もありますから、説明できるかどうかを前にもってくるのではなく、おもしろいことはおもしろいで、どんどんとりあげるのが〈たのしい教育流〉です。
引用はここまでとします。
➡︎ ここでたのしい教育メールマガジンのこれまでの記事タイトルが確認できます
毎日たのしい教育に全力投球、たのしい教育研究所(RIDE)です。みなさんの応援クリックが元気のバネです➡︎一緒に〈たのしい教育〉を広げませんか。簡単な方法があります。ここのクリックで〈応援している〉の一票入ります!
