秋の講座の一コマとしてM先生ペアが協力して「図工でたのしめる絵本シリーズ」を紹介してくれました。何冊も取り上げてくれたのですけど、この写真で紹介しているのが、五味太郎「らくがき絵本」です。
 五味太郎の「らくがき絵本」はわたしも大好きです。子ども達が大歓迎してくれる作品の一つです。
五味太郎の「らくがき絵本」はわたしも大好きです。子ども達が大歓迎してくれる作品の一つです。
教師をしている時は
・図画工作の時間
・家庭学習で
・お休みした先生の補充の時
・先生たちとのおたのしみ会
・理科で〈アイディアの出し方入門〉として
など、いろいろな時に利用していましたが、子ども達からの提案で〈学級活動のお楽しみ会〉の時にも利用したことがありました。
どういう絵本かというと、五味さんが、お題(絵のテーマ)と、絵を描いてくれているのですが、その絵が途中で終わっているのです。何も描いてなくて言葉だけ、というページもあります。子ども達がそれぞれのアイディアを駆使して絵を完成させる、という絵本です。
絵本のサブに「五味太郎50パーセント」という様なフレーズがありますが、M先生が出版社に電話して確認したところ「五味太郎が50パーセントは描いておきました」という意味だそうです。慣れないうちの子ども達だとそうかもしれませんが、しだいに子ども達が盛り上がってくると、子どもたちの描き込みが圧倒してきて「五味さんは10パーセントも描いていないな」という作品もたくさん出てくると思います。
テーマのひとつをみてみましょう。
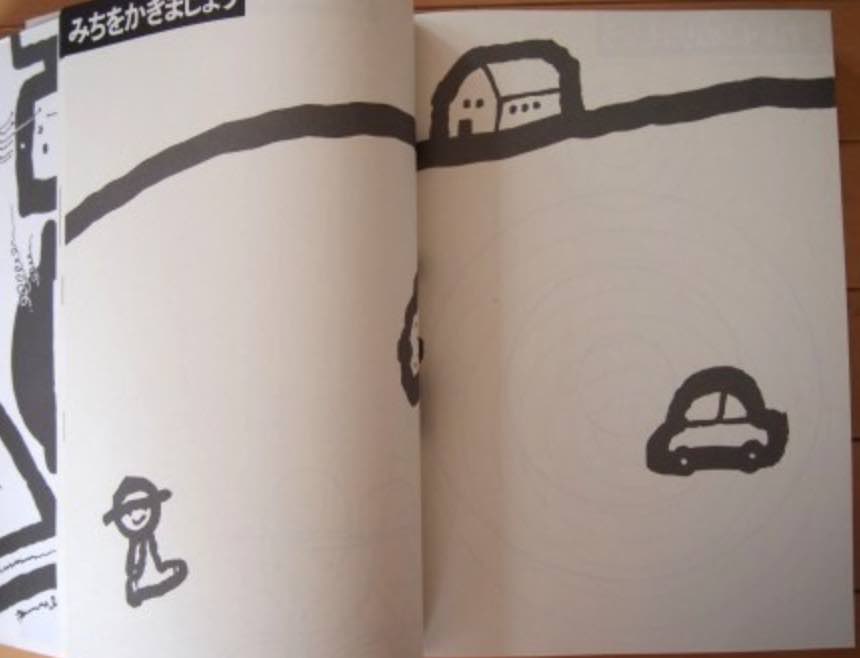
たとえば「みちをかきましょう」というテーマにこういう絵があります。子どもたちがこのあとをどんどん描いていくわけです。
 20年くらい前にわたしが書いたレポートがあって、その中にある作品を紹介します。
20年くらい前にわたしが書いたレポートがあって、その中にある作品を紹介します。
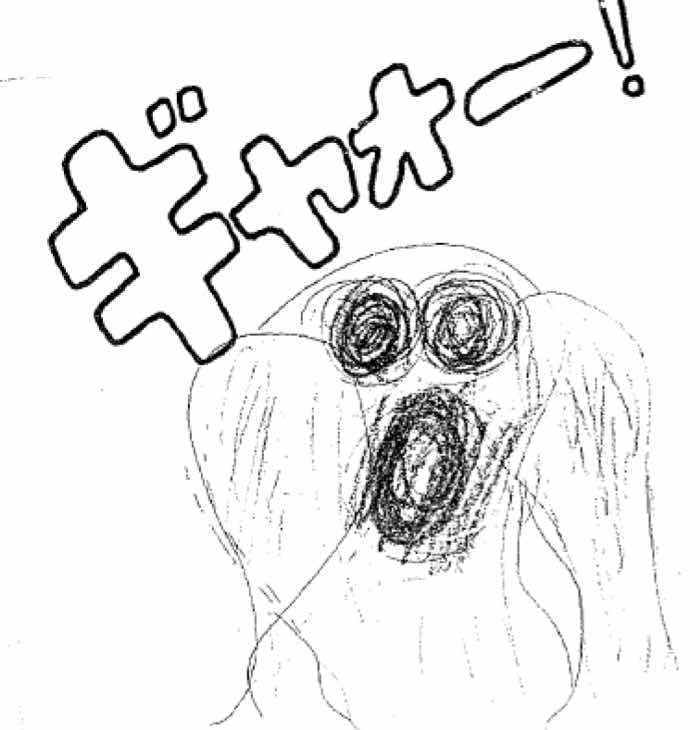
「ギャォー!」という文字から浮かんだアイディアを子どもたちが描き込んでくれたものです。元はカラーでしたが、モノクロ印刷版しか残っていません。残念なことですが、アイディアそのものは伝わるとおもいます。わたしは、みんなの判定で勝ち抜き戦方式でたのしんでいました。チャンピオンが決まるのですけど、その時のベスト3です。
第三位
第二位
一位
その時のチャンピオンは、ある女の子が描いたこの作品でした。
子ども達から「笑い声」や「おー」という声が上がったことを今でも覚えています。
絵もそうですけど、何と言ってもアイディアの勝ちです。
五味太郎 らくがき絵本 ブロンズ新書 お勧めいたします。
前回、ローレンツさんのお話を書いた時に「注文出来るコーナーがあると助かります」というメールもありました。五味さんの本が欲しい方は下からジャンプできます。二冊出ています。
たのしい教育広める活動をたのしくすすめる「たのしい教育研究所」です。 みなさんの応援をお待ちしています。 メールマガジンの購読も大いなる応援となります⇨こちら








 特別支援でいうインテグレーション教育は、ハンディのある子ども達も、そうでない子ども達も一緒に(統合して)教育しようという理念をもった言葉です。ですから「統合教育」という名前で呼ばれることもあります。普通学級の子ども達もハンディのあるクラスの子ども達も、ある教科では一緒になって学習する交流学習も普通に行われていますが、これもインテグレーション教育の流れです。今、学校で一般に行われている特別支援的な学習はまだインテグレーション教育の段階に止まっていることがおおいと思います。
特別支援でいうインテグレーション教育は、ハンディのある子ども達も、そうでない子ども達も一緒に(統合して)教育しようという理念をもった言葉です。ですから「統合教育」という名前で呼ばれることもあります。普通学級の子ども達もハンディのあるクラスの子ども達も、ある教科では一緒になって学習する交流学習も普通に行われていますが、これもインテグレーション教育の流れです。今、学校で一般に行われている特別支援的な学習はまだインテグレーション教育の段階に止まっていることがおおいと思います。
