クリスマスはヨーロッパに古くからあった〈冬至/とうじ〉を祝う日でした、と書いた記事に心動かされた方たちが何人もいて、長いおたよりを書いてくれた方もいました。その方への返事の中に書いたものを少し紹介しましょう。

「クリスマス」はキリスト教ができた時、その「冬至の祝いの日」をうまくとりこんだという話を書いたのですけど、キリスト教が生まれるまえから、ヨーロッパではずっと「ユール(スウェーデン語: jul、英語: yule)」というお祭りをしていた日でした、今でもクリスマスと言わず〈ユール〉と呼んでいるところもあるといいます。
ユール(スウェーデン語: jul、英語: yule)は、古代ヨーロッパのゲルマン民族、ヴァイキングの間で、冬至の頃に行われた祭りのこと。
のちにキリスト教との混交が行われたが、北欧諸国では現在でもクリスマスのことをユールと呼ぶ。
ウィキぺディア
https://ja.wikipedia.org/wiki/%E3%83%A6%E3%83%BC%E3%83%AB
それにしてもどうして冬至が嬉しいのでしょう?
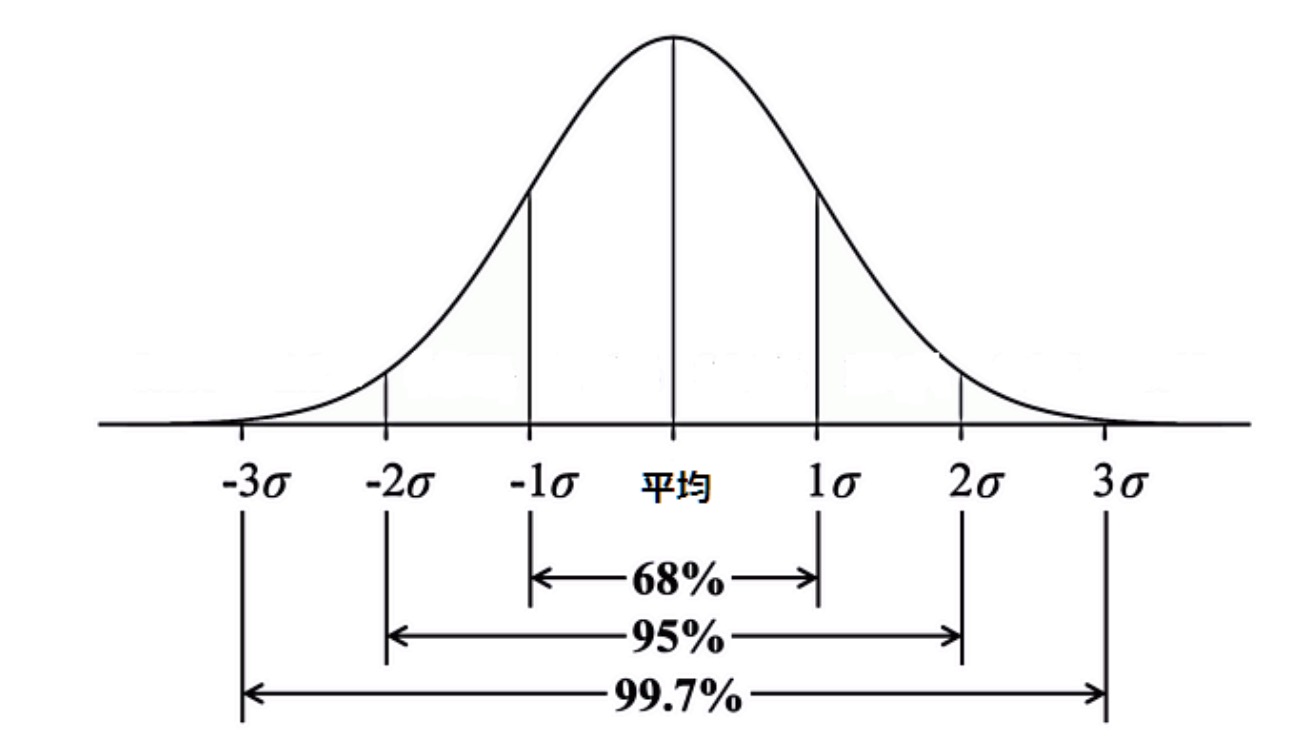
一年のうちで最も〈昼の時間が長くて夜の時間が短い〉のが「夏至/げし」で、最も〈昼の時間が短く夜の時間が長い〉のが「冬至」です。
明るい昼が短い日なのに、どうしてそういう日を祝うのか、不思議に思ったことはありませんか。
日々長くなっていく夜の闇が底をつく日だからです。
この日を境にして次第に昼の時間、太陽が地上を照らしてくれる時間が長くなっていくからです。
昔の人々は、その現象にうまく説明がつかないことのほとんどを〈神様〉のせいにしてきました。日の長さは〈太陽に向ける地球の角度〉がつくりだす現象だということは分からないので「この日を境にやっと太陽神が復活してくれるぞ」と喜んだのです。一年のうちでもとても嬉しい時なので、何日もかけて祝ったといいます。
冬至前後の北極圏の国々では、日中でも暗く太陽が沈んだ状態「極夜(きょくや)polar night」が続く。
冬至の頃に昇る太陽は非常に神聖で貴重なものとされ、人々は大いに太陽の復活を祝った。これがユール祭の始まりである。
https://www.worldfolksong.com/christmas/topic/yule.html
ヨーロッパにかぎらず、暗闇が長いことは事件や事故に巻き込まれる可能性も高くなるということです、命の危険も増えます。
植物にとっても、エネルギーの源である〈太陽の光〉をあびる時間が増えて光合成がすすみます。

北半球に住んでいる私たちには、冬至を境にこれからやっと太陽が姿を見せてくれます、私自身にとっても嬉しい日です。
沖縄もめずらしくとても寒い日々が続いているのですけど、これから日照時間が長くなるぞと考えて、元気にたのしくいきましょう。
② たのしい教育をより深く学び、より強く応援するための〈たのしい教育メールマガジン〉を一年間購読してみませんか。カウンセリングや講座、文章ドクター等の割引、教材購入の割引等の特典もあります