たのしい算数編〈分数を図で解く〉という記事が好評です、特に大人の皆さんの学び直しを含めて「おもしろいです!」というたよりがいくつも来ています、ありがとうございます。
自分で描いた図を送ってくださる方もいるので、私が描いた図を送っています。もちろんこれ以外は間違いということではありません!
一回目の練習問題として出した
〈3×1/2〉はどうして〈3/2〉になるのか
図を描いて解きましょう
です。
一回目に大切なことを書きました。
☆〈かける3〉というのは3倍(3セット)すること
☆〈かける1/2〉は〈2つに分けた一つ分〉にすること です。
図でみていきましょう。
まずこの正方形が〈1〉だとします。

〈かける3〉は3倍、3セットです。こうですね。
〈かける1/2〉というのは〈それを2つに分けた1つ分〉にすることです。
この矢印が1/2つまり2つに分けた1つ分(半分)の線です。

色をつけて見てみましょう、左の緑の部分がはじめに示した〈1〉です。真ん中の部分は〈1〉を2つに分けた1つ分、つまり1/2です。

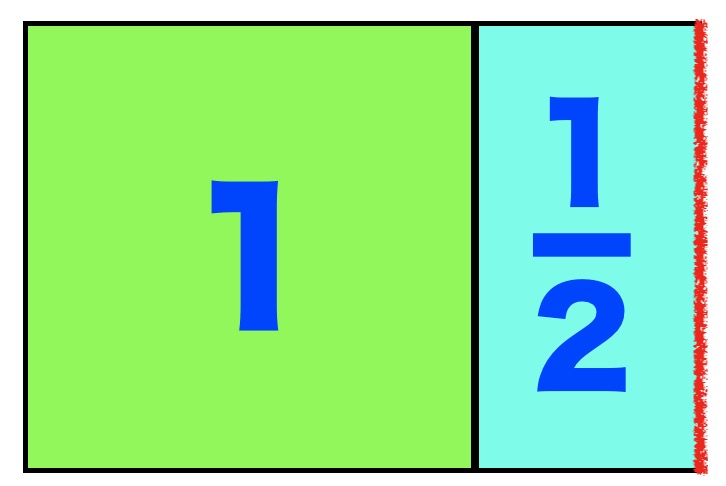
左の1は1/2ずつに分けることができますね。

1/2が3枚なので

図に戻すと、これは1枚と1/2つまり
 と表すこともできます。
と表すこともできます。
以上。
いかがでしょう。
分母は分母同士、分子は分子同士かけあわせればすぐに計算の答は出せるのに、どうしてこういう面倒なことをしているのか?
〈知恵〉とか〈賢さ〉というのは、こういう本質的なものがわかるということだからです。
計算の技法に長けて、スピードよくこなすことができることも意味がないことではありません。しかし〈本質はわからないけど解ける〉というのは「それが何を意味しているのかわからないけれど、計算ではこうなる」ということとです。極端にいうと「自分が何かを製造している過程で、身体に良いものを作っているのか、身体に悪いものを作ってるのかイミはわからないけれど、とりあえず製造物は出来上がった」ということにもにています。
自分がやっているものごとのイミを理解できるかできないか、それは決定的に重要なことなのです。そういう本質の部分が理解できる、その上で簡単な計算方法に則って手早く数処理する、そういうこども達を育てるのが「たのしい教育」です。
そう、どうしてこういう面倒なことをしているのか、のもう一つの答え、それは「これを読んでくれている皆さんがたのしんでくれているから」ということでもあります。本質的な内容、自分を高めてくれる、自分の可能性を開いてくれる何かを前にした時、人間はとてもたのしいのです。
たのしい教育に興味関心を持ってくださる方たちが、このサイトを知人に広報してくださることを期待しています。
たのしい教育全力疾走RIDE(たのしい教育研究所)、みなさんの応援が元気の源です。一緒にたのしく賢く明るい未来を育てましょう。このクリックで〈応援〉の一票が入ります!





