相変わらず〆切ものに追われていて日付が変わってから帰宅する日が続いています。こういう日々を強制されたら訴えられるでしょう。けれど自ら価値を感じてそういう日々を送ることができるのは幸せの形の一つです。

　さて前前回の〈たのしい学力向上〉で書いた〈かけざんの本質〉の話の反響がいくつも届いています。〈クランボルツ理論〉も好評です。

　今回は「自分で描いてみました」という人たちへの答えとして書かせていただきます。

　学校で「頭がいい」と言われている子ども達には「計算スピードの速さ」によってその評価を得ている子もたくさんいます。
　しかしそういうことで評価され日本の一流大学を受験する人たちも例えば
「１／２✕１／４ を図で説明して答えを出してください」という問題を出すと解けなかったという話を書きました。出典を思い出そうとしているのですけど、安野光雅の〈算私語録〉だったのか、森毅のエッセイだったのかなかなかはっきりしません。見つけ次第紹介します。

　それにしても優等生として育った学校の先生たちの多くも、同じ問題を出したときに、子どもが納得していくれるような答えを示すことが難しいということからも、その話信憑性が高いでしょう。

　前々回の練習問題として出した

1／2×1／4を計算ではなく図で描いて解答してください

を解いてみましょう。

　かけ算の本質については、前の項にもどって読み直してください、それがもっとも基本になります。

　まず１／２とはなにか？

１つのセットを２つに分けたその一つ分です。

これを〈1〉とすると

この左の部分が１／２です。

　それに１／４をかけるというのはどういうことか？

　4つにわけた一つ分にするということです、この赤の部分が１／２を４つに分けた一つ分です。
 

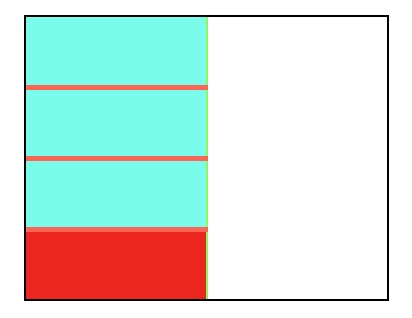
　この赤の部分は全体としてみると、どうなっているのか？
　１を８つに分けた１つ分になっていることがわかりますね。

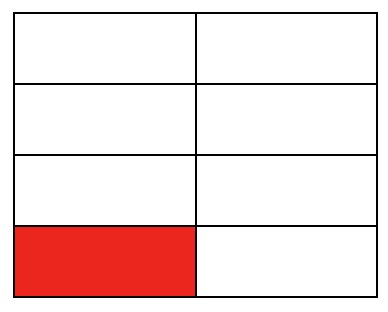これが　１／２×１／４＝１／８　の答えです。

　分子は分子にかけて、分母は分母同士かけるから１／８だと計算するのは早いのですけど、図で説明できる子は、さらに賢くなります。
　いろいろな問題を根本的に考えて答えを導き出そうという力が高まるからです。
　計算ではこうなるけど、本当にそうなのか？
 　それを答えをみて確かめるのではなく、自分で図を描いて確かめることができる、それはかなり賢い作業です。

　今度は ２／３➗１／２ を図で解く方法を考えてみませんか。

たのしい教育全力疾走ＲＩＤＥ（たのしい教育研究所）、みなさんの応援が元気の源です。一緒にたのしく賢く明るい未来を育てましょう。このクリックで〈応援〉の一票が入ります！

　季節の移ろいに合わせる様に美味しい野菜を届けてくださる〈たの研応援団員〉のＨさんがいます。昨日「いい野菜ができましたよ」とやって来てくれました。手に、ぎっしり詰められ、さらに上に重なってこぼれそうなほどのレタスをかかえて。

　袋の中には、こんなにみずみずしい野菜が顔をだしてくれます、そのままちぎって味見をすると、ほんわかと甘みを感じることができます。

　Ｈさんによると、引き抜いた後、土のついた根の近くは切って刻んで土に戻すそうです。土づくりから心をここめて育てているからこんなに新鮮で大きく美味しい野菜がそだつんですね。

　丹精込めた野菜を手にしながら語るＨさんは、まさに〈土と共に生きる人〉そのものです、でも本業は農業ではなく〈英語〉の実力を生かした仕事をしているんですよ。

　午後は、子ども会のメンバーと一緒に収穫体験をすることになっているそうです。

「野菜にカタツムリがついているのをみてキャーってびっくりする子もいるんですよ」

「引っ張って取るときに葉っぱがちぎれてしまったり、いろんなことがおこります」

とのこと、とてもたのしそうな顔をしていました。

　Ｈさんをみていると、野菜を育てることが、周りの人たちの笑顔を広げることと同じなのだと思えます。いっきゅう先生が最近「たのしい教育原理」という話を書いていました。たとえば〈野菜を育てること〉も「たのしい教育原理」との関連でみることができますね。

　研究所でサラダにして美味しくいただきました。箱からはみ出るほどたくさんの野菜たちは、仲間のところにも配りました。研究所にきてくれた方にもお分けしています。毎日たのしい、たのしい教育研究所です。

たのしい教育全力疾走ＲＩＤＥ（たのしい教育研究所）、みなさんの応援が元気の源です。一緒にたのしく賢く明るい未来を育てましょう。このクリックで〈応援〉の一票が入ります！

　小学校の頃、たのしい教育研究所で連続授業を受けたこどもたちが全員現役でいろいろな大学に合格してあいさつに来てくれたことを数回前に書きました。「どういう授業をしていたのですか」という質問が届いているのですけど、〈原子論〉や〈たのしい漢字学習〉などの他に算数で「〈1/2×1/3=1/6〉をいろいろな方法で説明してください」という授業をしたことを覚えています。私が小学校でやっていた授業なので思い違いがあるかもしれませんけど、算数の力がグッと高まりますから、みなさんも一緒に考えてみませんか。
　計算の仕方ではありません、つまり〈分母は分母にかけて分子は分子にかけるからだよ〉というのは答えではありませんよ。

　この問題を出したきっかけは、東京の某有名大学の入試で「〈1/2×1/3=1/6を計算ではなく図で描いて説明しなさい〉という問題を出したところ、他の難しい計算処理はできている受験生の多くが答えることができなかった」という話を聞いてからです。
　日本のトップクラスの大学を目指す人たちも〈数処理〉の基本概念ではなく、受験テクニックや計策テクニックなど、記憶を主にして入試を突破していくのだということへの大いなる疑問を出発点にしています。

　こどもたちには「いろいろな方法で説明してください」と投げかけましたが、ここでは図によって説明していく方法を紹介したいと思います。

　まず、自分自身で考えてみてください。

　保護者の皆さんは子どもが「ねぇお母さん、どうして ½✕⅓は1/6になるの？」と質問してきたと想定して考えてみましょう。

　さぁ、どうしてでしょう？

　あなたの考え！

たのしい算数の計算（かけ算の本質）

　〈かけ算〉とは何でしょう？

　たとえば〈✕２〉というのは、あるものが２セットになることです。

〈✕３〉というのは、あるものが３セットになることです。
 

では〈✕ ½〉はどういうことでしょう？
　「２つに分けた１つ分」にすることです。

〈✕ ⅓〉はどういうことでしょう？
　「３つに分けた１つ分」にすることです。

では〈 ½✕⅓〉というのはどういうことなのか？

　自分で図を描いてみませんか！

１／２ ✕１／３は「〈２つに分けた１つ分〉を〈３つに分けた１つ分〉にすること」です、こうです。
　まず一つのかたまり（全体の正方形）をタテに１／２にします、左半分の緑のバー　で表しています。

　その緑の部分今度はをヨコ（タテ割りが続くより見やすくなります）に３つに分けてみましょう、その一つ分が〈１／２ ✕１／３〉の答えです。
　ピースを数えてみてください、一つのかたまりを６つに分けた１つ分になっていますね。※正方形の左下、濃くなった部分です
　つまり〈１／２ ✕１／３〉は〈１／６〉ということです。

　学校でこういうレッスンはほとんどやっていないので、塾などでいい点数をとっているこどもたちも、なかなかできません。けれど、丁寧にそれを教えていくうちに「そうか、わかった」と喜んでくれます。

　練習してみましょう。

a．１／２✕１／４ を図で説明して答えを出してください（答は１／８）

b.　１／３×１／４ を図で説明して答えを出してください（答は１／１２）

c. 〈３×１／２〉はどうして３／２になるのか、図で説明してください

〈数量のイメージ〉を〈図で描きながら理解〉できるようになると単に〈計算方法〉で進めていく人たちより遥かに算数・数学のちからが高まります、私がすでに何度も実験済みです。

　なれていくと、１／２➗１／３ も図で答えを導き出せるようになります。いつかこのサイトで説明してみましょうね。

　学校では計算が得意な子は「頭がいい」と言われがちです。しかし〈図で描けるこどもたち〉のほうがずっと賢いのです。これからの本質的な学力向上に向けた重要なベクトルです。

たのしい教育全力疾走ＲＩＤＥ（たのしい教育研究所）、みなさんの応援が元気の源です。一緒にたのしく賢く明るい未来を育てましょう。このクリックで〈応援〉の一票が入ります！

　計画的偶発性理論（Planned Happenstance theory）という名前を聞いたことがあるでしょうか、心理学者クランボルツが提唱した理論です。のちに〈Happenstance Learning Theory〉と名称を変えています、和訳がまだ広まっていないので〈偶発性学習理論〉と名付けておきます。「クランボルツのキャリア理論」としておいてもよいでしょう。

　沖縄県からの依頼で県内の親子向けにキャリア教育の授業を引き受けたり、予算を組んでもらって県内の学校向けのキャリア教育副読本を作成している時入手した本や資料の中で「まさに〈たのしい教育〉だ」と感じていたのが計画的偶発性理論です。

　板倉聖宣が「たのしい授業」を提唱して後、松本キミ子（故人）さんのキミ子方式と出逢い『楽しい授業』として広く紹介した様に、計画的偶発性理論はキャリア教育に関わる重要な理論で〈たのしい教育〉の原理から派生する理論だとみることができます、クランボルツの方が有名ですけど。
　とはいえ、有名さの大小が理論的順位を決めるのではありません。より原理的なものがたのしい教育なのです。

０.現在の教育は、その子の目標や夢に向かって努力し、それを成し遂げることを想定している

１.しかし、成功した人々の人生をたどってみると、その多くは〈偶然性〉に左右されていた。すてきな英語の先生に出会ったから英語が好きになった人がいたり、私の様に中学で学ぶと同時に英語が大嫌いになったり、趣味で偶然出会った人のアドバイスでその職業についたり

２.そういう偶然性によるものを〈縁〉とか〈ラッキーなこと〉にするのではなく、自然に任せるのではなく積極的に活かせるような教育が大切である。たまたま出会ったチャンスを自分の人生にプラスに活かせるのはどういう人間か？

（1）「好奇心」 ――行動を狭く限定せずいろいろなものに興味関心をもつ力
（2）「持続性」 ―― すぐに投げ出さず一定期間は継続して結果をみることができる力
（3）「楽観性」 ―― どうせダメだと考えずポジティブに捉える力
（4）「柔軟性」 ―― ある考え方等に固執せず起こるできごとや状況に柔軟に対応する力
（5）「冒険心」 ―― ある程度のリスクがあっても挑戦できる力

こういう力をもったこどもたちをそだてようではないか。

　そういう理論です。

　まさに〈たのしい教育〉が提唱する「自分の興味関心を大切にして、いろいろな予想を立て挑戦するこどもたち先生たち大人たち」を育てる活動です。〈たのしい教育〉の「キャリア教育分野」だといってもよいでしょう。

　大きな報告ものが一区切りついたので、週一度のメールマガジンにさらに詳しくまとめはじめています。

たのしい教育全力疾走ＲＩＤＥ（たのしい教育研究所）、みなさんの応援が元気の源です。一緒にたのしく賢く明るい未来を育てましょう。このクリックで〈応援〉の一票が入ります！